エクセルで標準偏差を使いこなす！求め方からグラフの作成までを解説

統計学で利用される「標準偏差」という言葉をご存知でしょうか。高校数学でも学習する内容のため、一度は耳にしたことがあるかもしれません。この標準偏差は、ビジネスシーンでも頻繁に活用されるデータです。今回の記事では、エクセルを用いて標準偏差を簡単に計算する方法や、求めたデータをグラフ化する方法について解説します。

サンプルデータを使って練習がしたい・・・という方向けに、本記事で使用しているデータをダウンロードできるようにご準備しております！こちらからダウンロードしてみてください。

標準偏差の概要

統計的な数字として用いられる標準偏差ですが、どのような意味を持つ数値なのでしょうか。この項目では標準偏差についての理解を深めるために、標準偏差の意味や数学的な計算方法について解説します。

　

標準偏差の意味｜平均とのズレを数値化したもの

標準偏差とは、データが平均値からどの程度ずれているかを示す統計的な指標です。ビジネスにおいても活用場面は多くあり、一例としては以下が挙げられます。

• 品質のばらつきを数値化することで行う、統計的な品質管理
• 販売数の可視化による、安全在庫の管理

標準偏差の値が大きくなると、平均値からのばらつきが大きいことを表します。例えば、品質管理の場合においては、「でき上がった製品ごとの品質の差が大きい」と判断することが可能です。

手計算で標準偏差を求める方法　

標準偏差は、対象となるデータの値と平均値との差を二乗して、その総和をデータの数で割ったものが持つ正の平方根です。標準偏差を求める手順は以下の通りです。

1. データ全体の平均値を求める
2. 各データから平均値を引いた値を求める（この値を「偏差」と呼ぶ）
3. 各偏差を二乗する
4. 二乗された偏差の合計を求める
5. 4の結果をデータの総数で割る（この値を「分散」と呼ぶ）
6. 分散の正の平方根を求める

手計算では煩雑になりやすい標準偏差の計算も、エクセルを用いれば簡単に行えます。次の項目以降では、計算方法やグラフの作成方法を詳しく解説します。また、標準偏差は統計学において一般的に用いられる数値です。そのため、前提として統計学の知識があると、「自分が標準偏差を求めたい母集団においてどの関数を用いることが適しているか」の判別がつきやすいでしょう。

標準偏差を含む統計学について学習したい方は、チャンネル登録者数36万人のYouTubeチャンネル「ユースフル/スキルの図書館」の動画をご覧ください。

エクセルの関数を使って標準偏差を求める3つの方法

エクセル関数で標準偏差を求めるには「STDEV」とつく関数を利用します。STDEVとつく関数は大きく2つに分けられており、それぞれが派生したものを合わせて合計4種類あります。これらの関数は、主に因数をどのように扱うかという面で違いがあります。

①STDEV関数を用いた標準偏差の求め方

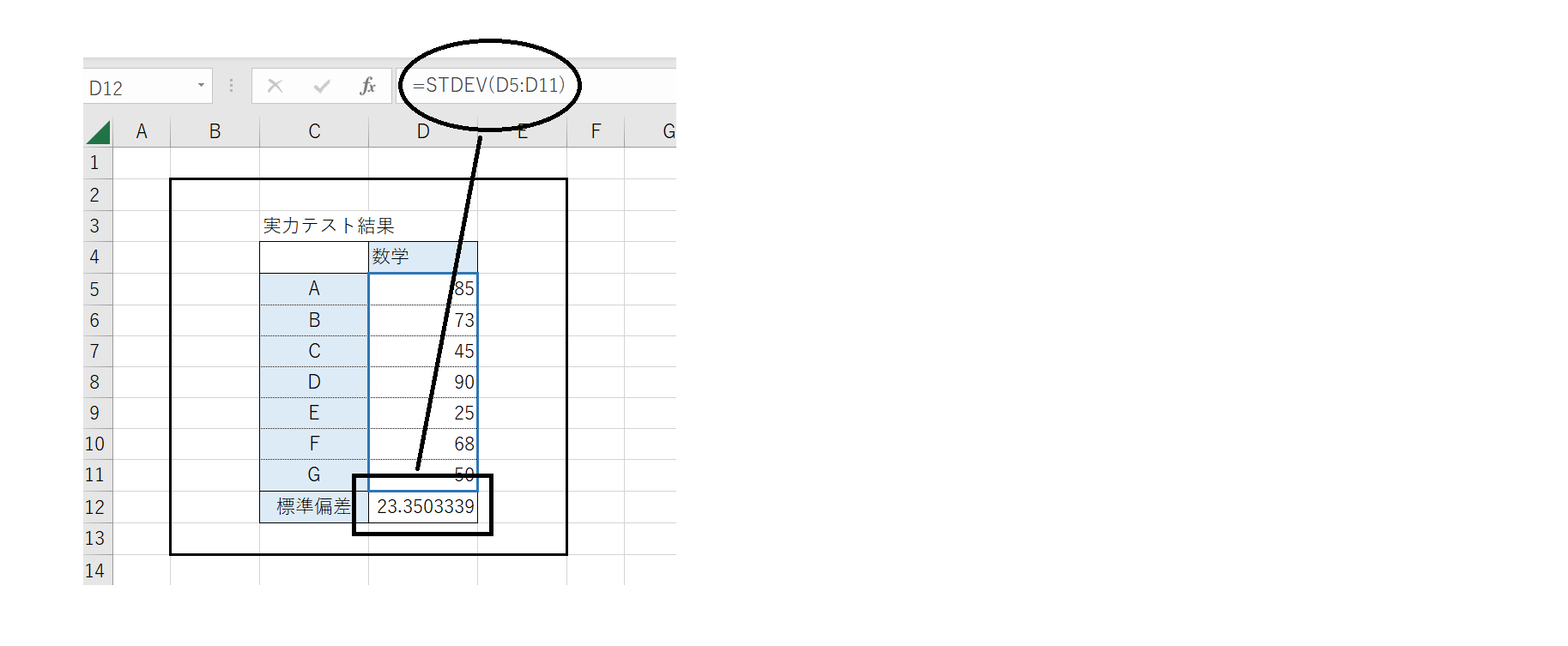
標準偏差を求める関数の1つ目はSTDEV関数です。エクセル2010以降のバージョンでは「STDEV.S」に置き換えられましたが、エクセル2010以前のバージョンとの互換性が必要な場合は「STDEV」を利用できます。STDEV関数で求められる値は「不偏標準偏差」です。母数全体が不明な場合に、母数の標準偏差を予測します。

このSTDEV関数では、あくまで母数全体は不明であるという扱いになるため、データは「標本」として扱われます。数式の記載方法は以下の通りです。

②STDEV.P関数を用いた標準偏差の求め方

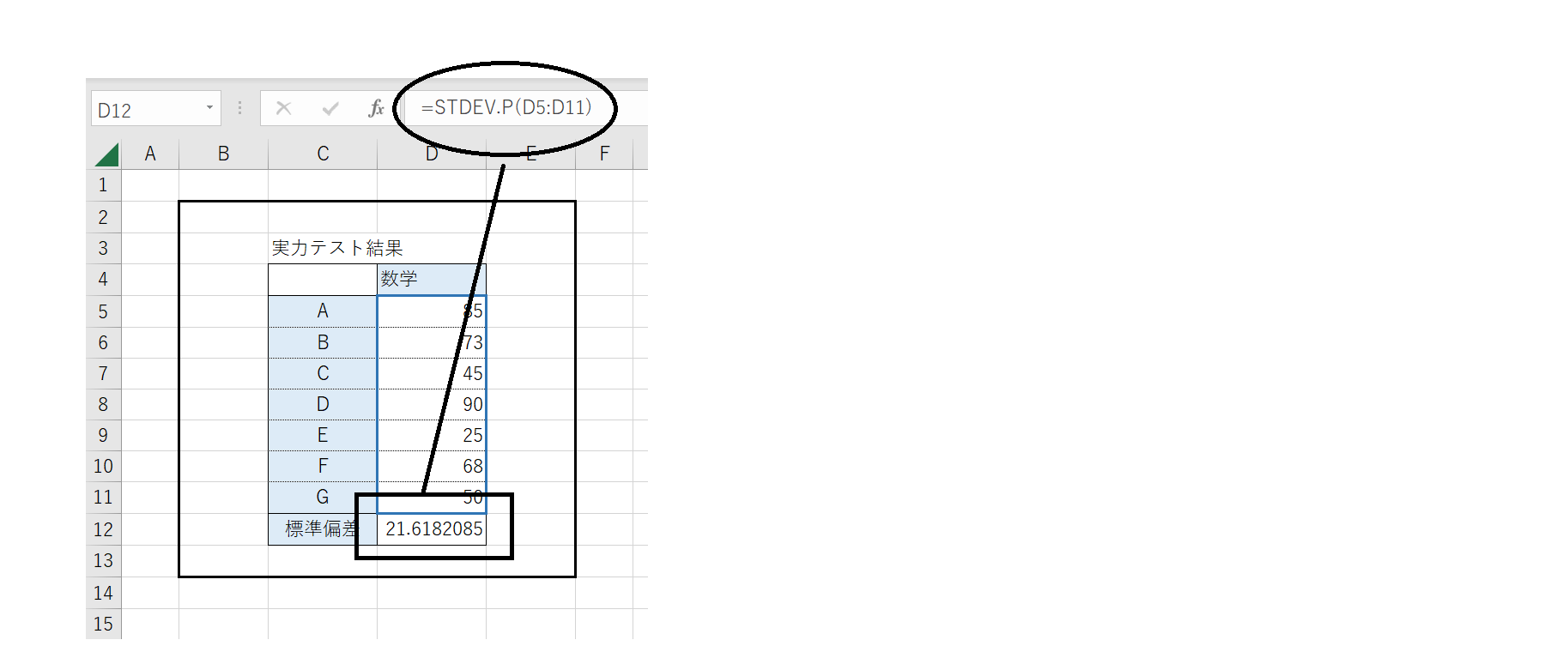
標準偏差を求める2つ目の関数は「STDEV.P関数」です。STDEV.P関数は、用意したデータの標準偏差を求めたい場合に使用します。用意されたデータが母集団全体のデータではなく一部分である場合には、前述のSTDEVを使用しましょう。数式の記載方法は以下の通りです。

［=STDEV.P(データ範囲)］

上記のデータ範囲は「母数」として扱われます。一般的な統計では、「母数が不明であるが、標準偏差を求めたい」というケースが多くなるため、STDEV関数を利用するシーンが多いといえるでしょう。

③STDEVA関数を用いた標準偏差の求め方

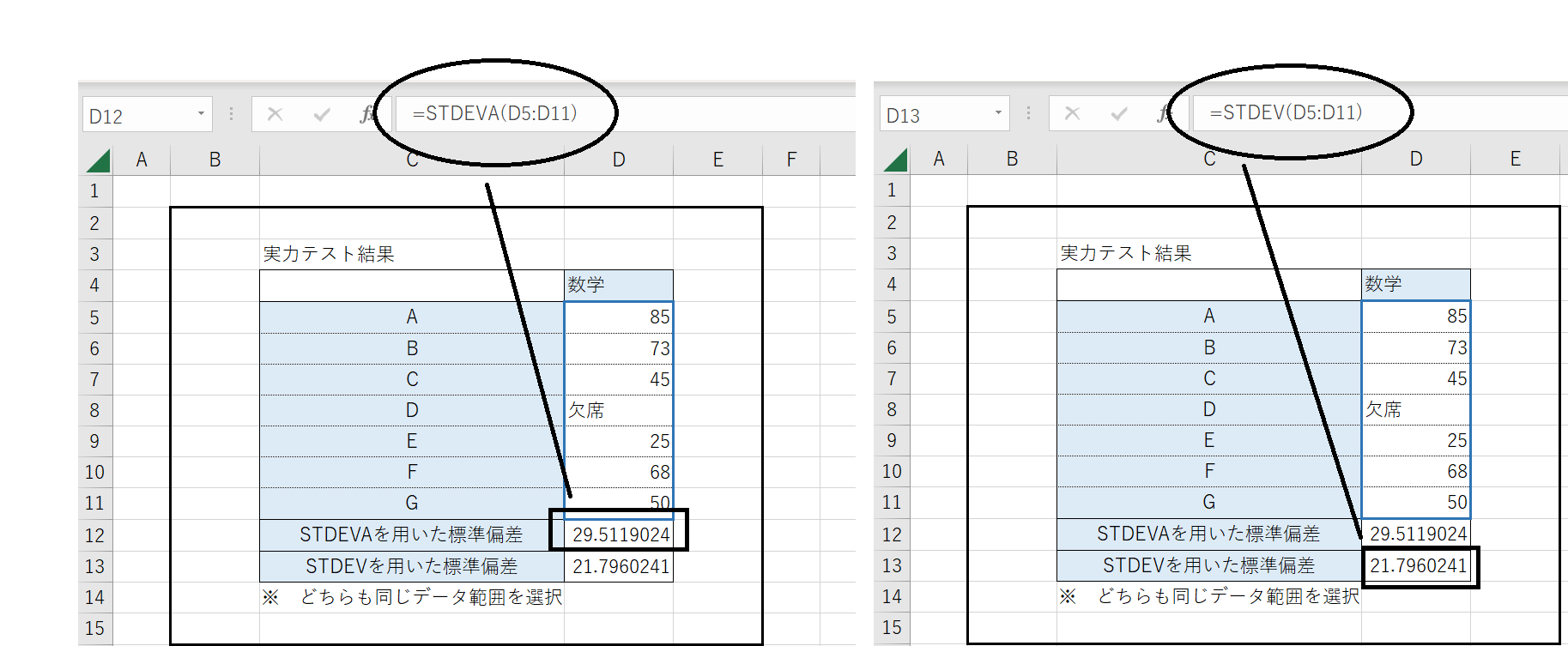
標準偏差を求める3つ目の関数は「STDEVA関数」です。STDEVA関数は、STDEV同様、「標本」を対象として標準偏差を求める関数です。データに文字列が入っている場合には、計算結果が異なります。

• STDEV：文字列を無視して計算
• STDEVA：文字列を”0”として計算

例えば、実力テストの結果において、欠席者をカウントせずに計算するか、欠席者の得点をゼロとして計算するかによって、平均点や標準偏差は異なります。STDEVとSTDEVAを適宜使い分けるとよいでしょう。また、「STDEV.P」に上記の仕様を適用した「STDEVPA」という関数もあるため、必要に応じて使い分けられると、欲しいデータをすぐに求められます。

数式の記載は、以下の通りです。

［=STDEVA（データ範囲）］

標準偏差をエクセルのグラフで示す3つの方法

標準偏差が大きくなるほど、データが平均値から大きくばらついていることを示します。反対に、標準偏差が小さい場合は、ばらつきも小さいと判断できます。エクセルで算出した数値だけではわかりづらいという場合は、グラフを使って可視化をすることが有効です。

①棒グラフを利用する方法

標準偏差のエラーバー付き棒グラフを作成することで、ばらつきを可視化できます。

【用意するデータ】

• 平均値
• 標準偏差

【作成手順】

1. ［Ctrl］を押しながら、データタイトルと平均値の範囲を選択
2. ［挿入］→［グラフ］→［おすすめグラフ］の順にクリック
3. ［集合縦棒］を選択して［OK］をクリック
4. 上部メニュー左側［グラフ要素の追加］を選択し、［誤差範囲］、［その他の誤差オプション］の順にクリック
5. ［ユーザー設定］にチェックを入れ、［値の選択］をクリック
6. ［正の誤差の値］［負の誤差の値］それぞれの矢印をクリックし、標準偏差の範囲を指定

この手順でグラフが完成します。棒グラフ上にあるエラーバーが平均値からのばらつきを表しています。

②散布図を使う方法

散布図にも、棒グラフ同様に標準偏差のエラーバーをつけられます。

【用意するデータ】

• 平均値
• 標準偏差

【作成手順】

1. ［Ctrl］を押しながら、データタイトルと平均値の範囲を選択
2. ［挿入］、［グラフ］の順にクリック
3. ［散布図（直線とマーカー）］を選択し［OK］をクリック
4. ［グラフ要素の追加］を選択し、［誤差範囲］、［その他の誤差オプション］の順にクリック
5. ［ユーザー設定］にチェックを入れ、［値の選択］をクリック
6. ［正の誤差の値］［負の誤差の値］それぞれの矢印をクリックし、標準偏差の範囲を指定
7. 横のエラーバーは不要なので［Delete］で削除

この手順でグラフが完成します。各項目上のエラーバーが平均値からのばらつきを表しています。

③正規分布曲線を使う方法

　

正規分布曲線は、平均値を中央にしたグラフで、模擬試験の偏差値をグラフ化するときによく利用されるグラフ形式です。以下の方法で作成できます。

【用意するデータ】

• 平均値
• 標準偏差

※例では、平均値を63.2、標準偏差を7として、2点刻みの素点データを用意しています。

【グラフ作成手順】

1. ［=NORM.DIST(データの値,平均点,標準偏差,FALSE)］で正規分布の値を求める
2. 正規分布曲線を作成するデータエリアを選択
3. ［挿入］、［グラフ］の順にクリック
4. ［散布図（平滑線とマーカー）］を選択し［OK］をクリック

「NORM.DIST関数」を用いて正規分布の値を求めることで、平均値を中央としてそれぞれの値が位置する場所を示すグラフを作成できます。

まとめ

データが平均値からどの程度ばらついているかを数値化する標準偏差は、模擬試験の偏差値のみではなく、ビジネスシーンでも活用できます。エクセルの関数を用いて簡単に求められるほか、グラフを作成して可視化することも可能です。関数の特徴ごとに使い分けることでより、多様な分析ができるようになります。

「面倒な業務を効率化して残業を減らしたい」
「プロのExcel技を身に着けて社内で頼られる存在になりたい」

そんな方にはユースフルの公式LINEがオススメです！元伊藤忠商事経理でExcel実務のプロ、長内孝平（おさ）が運営しており

• Excel/PowerPointなどPCショートカット288選PDF
• Excel無料講義動画480分
• ユースフルの講座割引クーポン

などLINE会員限定の豪華4大特典を無料でプレゼント中です！ぜひコチラ↓の画像をタップして受け取ってくださいね！